I still say to myself when I am depressed and find myself forced to listen to pompous and tiresome people: “Well, I have done one thing you could never have done, and that is to have collaborated with Littlewood and Ramanujan on something like equal terms.”
A Mathematician’s Apology (1941). G.H. Hardy (1877-1947)
Mathematics as the great equalizer
What do many of the most successful (and richest) hedge fund managers have in common with a life-long homeless person? That they have worked together, on equal terms, in solving some of the hardest mathematical questions.
Yes, in a stratified world with increasing wealth inequality, gated communities and elite clubs, where the ultra-wealthy rarely interact with the poor, many of the richest people on Earth are mysteriously connected to a vagabond who played a critical mentor role in their careers. But in this story the pauper did not want to become a prince. In fact, the pauper methodically donated all the money he ever received for his achievements.
The pauper
Paul Erdős (1913-1996) was one of the most prolific mathematicians in history. Over his lifetime, he published a staggering 1,525 journal articles and collaborated with 511 colleagues, all without institutional support or holding an academic position. Paul carried two half-empty suitcases around the world, which contained all his earthly possessions. He would stay in a co-author’s house for a few weeks per visit, just enough time to make a new mathematical breakthrough, before moving on to the next fortunate host. One of his mottos was “another roof, another proof.”
 Paul Erdős inspired generations of mathematicians, of all ages. In this 1985 photo, Erdős explains a problem to Terence Tao, who was only 10 years old at the time. Tao received the Fields Medal in 2006
Paul Erdős inspired generations of mathematicians, of all ages. In this 1985 photo, Erdős explains a problem to Terence Tao, who was only 10 years old at the time. Tao received the Fields Medal in 2006
Paul Erdős made important contributions to a wide range of subjects, and was awarded the prestigious Wolf Prize (1983/84) among a long list of honors. However his place in mathematical history is well secured for another exceptional reason. His most important “proof” is perhaps that mathematicians can work effectively through vast collaboration networks. Until recently, mathematics was essentially a “lone wolf” quest. Collaboration was rare, and authors tended to hide zealously their discoveries until they were ripe for publication (think of Newton and Leibniz). Today, mathematicians are interconnected, coordinate efforts and borrow ideas from each other, sometimes devoting hundreds of brains to proving the same conjecture. Can dozens of good mathematicians work together like a great one? Surprisingly, the answer is yes! Visit the Polymath project for astonishing examples of discoveries involving hundreds of co-authors.
Understanding Erdős numbers
Erdős was involved in so many different mathematical endeavors, that some colleagues humorously wondered, who is not somehow working with him? Hence the idea of “Erdős number” (E#) was born. E# is the length of the shortest collaboration path between a mathematical author and Erdős. If David has co-authored a paper with Erdős, David has E#1. If Mark has co-authored a paper with David, Mark has E#2 (or E#1, if Mark co-authored directly with Erdős), and so on. If there is no collaboration path between Peter and Erdős, Peter’s E# is infinite. The American Mathematical Society offers a free online tool that computes E#, and Oakland University’s Erdős Number Project hosts a wealth of resources.
This notion of E# first started in the year 1969 as a tribute to Paul Erdős by colleagues and friends, without envisioning it as a research tool. However, over the decades academic studies on E# distributions have found interesting features about how mathematical discoveries take place. Out of the ~401,000 mathematical authors (since the 1930s) listed in MathSciNet, over 67% have a finite E#. Being listed in that authors’ catalog is in itself an achievement, because it means that the researcher made a mathematical discovery that was peer-reviewed and published in a journal indexed by MathSciNet. Also, note that ~401,000 authors over roughly 90 years is a relatively small number, considering the millions of people who receive a STEM degree every year. The median E# across these accomplished mathematicians is 5, with an upper bound of 13. Every winner of the Fields Medal has a finite E#, with a median of 3, a statistically significant divergence from the overall population. Every winner of the Abel Prize has a finite E#, with a median of 3 and an average of 2.94. Every winner of the Nevanlinna Prize has a finite E#, with a median of 2 and an average of 2.4.
About 80% of Nobel Laureates in Physics also have finite E#, including Albert Einstein (E#2), Enrico Fermi (E#3), Wolfgang Pauli (E#3), Max Born (E#3), Richard Feynman (E#3), Hans Bethe (E#3), etc. Srinivasa Ramanujan has an E#3, albeit Erdős was only 7 years old when the Indian genius tragically died. That is because G.H. Hardy, Ramanujan’s mentor and co-author, has an E#2. Good mathematicians tend to collaborate with other good mathematicians. Like in sports, the better a “player” becomes, the more he is pursued by colleagues who want him to join an existing team, and work together on a challenging problem. Strong teams do not chase weak players, and strong players do not join weak teams. As the collaboration network coalesces and becomes denser around great mathematicians, the chances to connect with the center (E#0) grow dramatically.
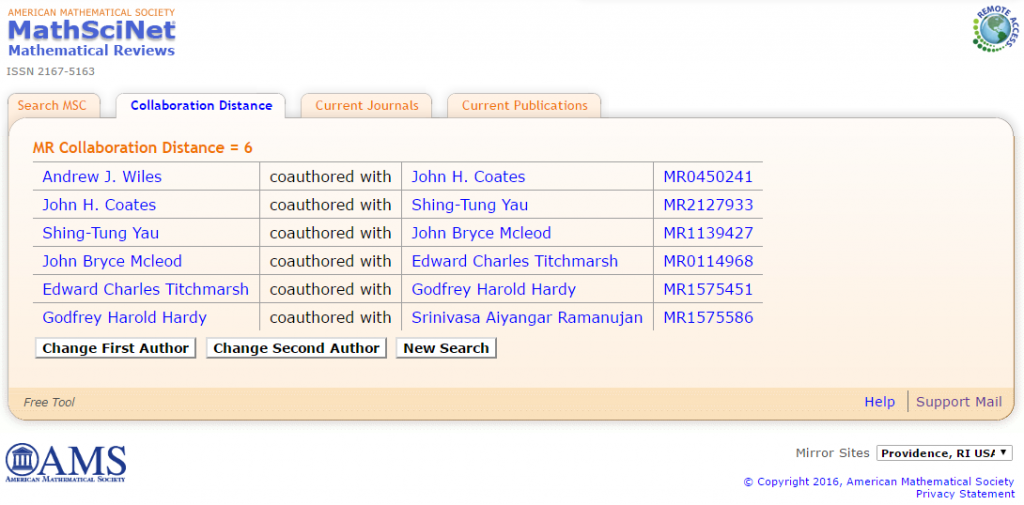 Good mathematicians tend to work with other good mathematicians. There is often a collaboration path between any two great mathematicians, regardless of age, nationality, ethnicity or social background… even spanning centuries. The figure above shows a path connecting Sir Andrew J. Wiles (E#3) with Ramanujan (E#3), through an all-star sequence of Fields medalists and Fellows of the Royal Society
Good mathematicians tend to work with other good mathematicians. There is often a collaboration path between any two great mathematicians, regardless of age, nationality, ethnicity or social background… even spanning centuries. The figure above shows a path connecting Sir Andrew J. Wiles (E#3) with Ramanujan (E#3), through an all-star sequence of Fields medalists and Fellows of the Royal Society
Does this mean that E# measures mathematical prowess? Not necessarily. If we search hard enough, we may find highly-cited mathematicians who have made breakthroughs on their own. It is fair to say that E# measures a combination of these two ingredients: Proficiency and collaborative skills. A skillful mathematician working alone will have an infinite E#, and a very social but mediocre mathematician will have a hard time publishing in a MathSciNet-indexed journal, plus finding co-authors in the proximity of Paul Erdős.
The princes of quantitative finance
A large portion of the most successful investment funds in history are led by mathematicians. Many of those “quant” firms have been either founded or managed by mathematicians with low E#. The following table provides an incomplete list.
| Name | Firm | Position | E# |
| Elwyn R. Berlekamp | Axcom Trading Advisors | President | 2 |
| Marcos Lopez de Prado | AQR Capital Management | Partner | 2 |
| Peter J. Weinberger | Renaissance Technologies | Managing Director | 2 |
| James B. Ax | Axcom Trading Advisors | Founder, CEO | 3 |
| Leonard E. Baum | Axcom Trading Advisors | Chief Scientist, Founder | 3 |
| Jean-Philippe Bouchaud | Capital Fund Management | Chairman | 3 |
| Vincent Della Pietra | Renaissance Technologies | Managing Director | 3 |
| Alexander Lipton | Bank of America Merrill Lynch | Managing Director | 3 |
| James H. Simons | Renaissance Technologies | Founder, CEO | 3 |
| Glen T. Whitney | Renaissance Technologies | Managing Director | 3 |
| John Overdeck | Two Sigma | Founder, Co-CEO | 4 |
| Marc Potters | Capital Fund Management | Co-CEO | 4 |
| David E. Shaw | D.E. Shaw | Founder, CEO | 4 |
| Anthony W. Ledford | Man AHL | Chief Scientist | 4 |
| Stephen Della Pietra | Renaissance Technologies | Managing Director | 4 |
| Lalit R. Bahl | Renaissance Technologies | Senior Researcher | 4 |
| Alexey V. Kononenko | Renaissance Technologies | Managing Director | 4 |
| Alexander Astashkevich | Renaissance Technologies | Senior Researcher | 4 |
| Alkes L. Price | Renaissance Technologies | Managing Director | 4 |
| Nicholas Patterson | Renaissance Technologies | Managing Director | 4 |
| George Zweig | Renaissance Technologies | Senior Researcher | 4 |
| Peter Brown | Renaissance Technologies | Co-CEO | 4 |
| David J. Hand | Winton Capital Management | Chief Scientist | 4 |
| Charles-Albert Lehalle | Capital Fund Management | Senior Research Advisor | 4 |
| Neil A. Chriss | Hutchin Hill | Founder, CEO | 5 |
| Robert B. Litterman | Kepos Capital | Chairman | 5 |
| Alexander Belopolsky | Renaissance Technologies | Senior Researcher | 5 |
| Robert J. Frey | Renaissance Technologies | Managing Director | 5 |
Of course one reason for this is, sophisticated mathematical models help beat the collective wisdom of the markets. But as explained earlier, E# measures more than mathematical prowess. It also accounts for collaborative skills. Mathematicians that are used to work as part of a research network exhibit behavioral traits that should be useful in the corporate world. Cracking the market’s fortune formulas is definitely a complex team effort that requires dozens of individuals working together, complementing each other. This combination of collaborative skills with mathematical proficiency, as measured by E#, is the stronger predictor of investment performance.
Collaborating effectively is not easy in mathematics, and should not be discounted as a common skill. It requires being able to share complex ideas in a respectful, objective and rigorous way. If understanding advanced math is hard enough, understanding cutting-edge in-the-making math is quite a feat. In addition, brilliant people often prefer to pursue their own ideas rather than embrace someone else’s in a collaborative effort. The ability to lead and persuade others to join an obscure intellectual struggle is rather uncommon.
As it is often the case in mathematics, the concept of E# was proposed without ever suspecting its future applications. The inventor of E# could not have envisioned that this notion would connect some of the richest people in the world, the princes of quantitative Finance, with good old Paul Erdős. As for the pauper of this story, he had the traits that make a great prince … if only he cared about earthly matters.