
Machine learning in finance
In recent years, machine learning techniques and big-data facilities have become quite popular in the finance and investment world. In the wake of this success, numerous machine learning researchers have decided to found their own asset management companies, hoping to capitalize on this trend.
This begs the question: Are large amounts of data and computing power all that is needed to tame the markets? In this article we delve into the uses and misuses of machine learning (ML) in finance.
The two kinds of machine learning
To the neophyte, all ML might look like the same. However, there is a clear distinction between two ways of applying ML. One category is exemplified by the commercial applications developed by industry titans such as Google, Facebook, Amazon, Netflix, Apple, Microsoft and Tesla. Those firms have a clear goal: Producing oracles, that is, “black boxes” that make the best predictions regardless of how that is achieved. When Amazon recommends a book for you, the oracle is not developing a general theory of human behavior, with preferences that might be useful in a wide range of settings. Instead, that oracle is mining large amounts of data to find a pattern that somehow chooses a book that hopefully will be of interest to you in particular. This is the kind of practical ML with which the general public is most familiar.
A second category is the typified by the ML utilized in scientific research, ranging from scientists at large research laboratories such as the Lawrence Berkeley National Laboratory in the U.S. and INRIA in France, to the countless individual researchers at universities worldwide. The goal of the ML techniques employed by these researchers is very different: analyzing data, identifying “interesting” phenomena worthy of further study, and, ultimately, producing better scientific theories. A good research scientist would not exchange a good theory for the best of oracles. The ultimate purpose of science is not to make predictions or recommend books; although predictions are useful to test and validate theories, the ultimate goal of research is understanding nature. In contrast, oracles keep us in the dark. An oracle does not advance knowledge, nor can we build knowledge upon an oracle, refine it or generalize it. We could have an oracle for predicting the behavior of electric fields, and another oracle for predicting the behavior of magnetic fields, and yet still miss the essential fact that electromagnetism is a single physical phenomenon.
The reasons financial oracles fail
One could argue that oracles are an ideal application for finance: An investor just wants the returns. Why would she concern herself with economic theories? The problem is that investing is an activity that cannot be tackled effectively by oracles, for multiple reasons. First, oracles thrive at tasks where there are millions of independent examples an algorithm can learn from, and where new datasets can be generated on the fly. You can train an algorithm on millions of faces, and there will be billions more to draw from. In contrast, financial series are generally short and highly redundant (multicollinear).
Second, ML algorithms rely on assumptions that are typically violated by financial series. For example, financial series are often nonstationary. In the context of time series, nonstationarity means that the series are not characterized by a constant distribution across time. Nonstationarity is a big problem, because an ML algorithm can only learn the characteristics of examples if they are comparable. It would be the equivalent of training an algorithm to recognize cat faces and, along the way, start feeding it dog faces mislabeled as cats.
Third, the signal-to-noise ratio in financial markets is very low, because of arbitrage forces. Those competitors whose mistakes we profit from will either learn or disappear, leading to the erosion of that source of profits. In contrast, physical laws are not “arbitraged away.”
Fourth, we cannot repeat experiments in a laboratory, while changing the environmental variables, in order to identify a particular cause-effect mechanism. For instance, we cannot repeat the flash crash of 6 May 2010 thousands of times by adding and removing specific players until we isolate a cause. All we have is the one-path historical phenomenon observed on that particular day.
As a consequence, oracles are generally not very useful in finance. It would be most unwise to take an algorithm from a Kaggle competition, plug it into a set of financial time series, and expect it to predict financial prices. There is skill involved in picking the right financial question that an algorithm may help answer. Theoretical knowledge is essential for setting realistic and coherent assumptions. Financial knowledge is needed to prepare the data correctly, and interpret intermediate results.
“What makes an asset useful?” — A case study in overfitting
Numerous ML researchers have approached financial markets according to the “oracle paradigm.” A close look at these studies exposes the pitfalls of such an approach. For example, consider a blog article and paper recently published by a Silicon Valley startup that develops ML algorithms for financial markets, largely devoid of economic theory.
In a nutshell, the article states that “[i]t is impossible to test whether a time series is non-stationary with a single path observed over a bounded time interval — no matter how long,” therefore “you shouldn’t trust any stationarity test.”
For trained mathematicians, these bold statements raise several red flags. Stationarity tests are mathematical devices. They are proved to work, under certain clearly stated assumptions. But rather than attacking the validity of the assumptions in finance, this organization dismisses the validity of the tests themselves. In their own words:
“Intuitively, a stationary time series is a time series whose local properties are preserved over time. It is therefore not surprising that it has been a pivotal assumption in econometrics over the past few decades, so much so that it is often thought that practitioners ought to first make a time series stationary before doing any modeling, at least in the Box-Jenkins school of thought. This is absurd for the simple reason that, (second order) stationarity, as a property, cannot be disproved from a single finite sample path. Yes, you read that right! Read on to understand why.”
Most scientific predictions rely on the assumption that prediction errors are stationary. Consequently, stationarity tests play a critical role across all fields of science. Finding an error in the mathematical proofs that support any of these tests would be an earthshaking discovery, perhaps not garnering a headline in the front page of the New York Times, but very significant nonetheless. But how could that be true?
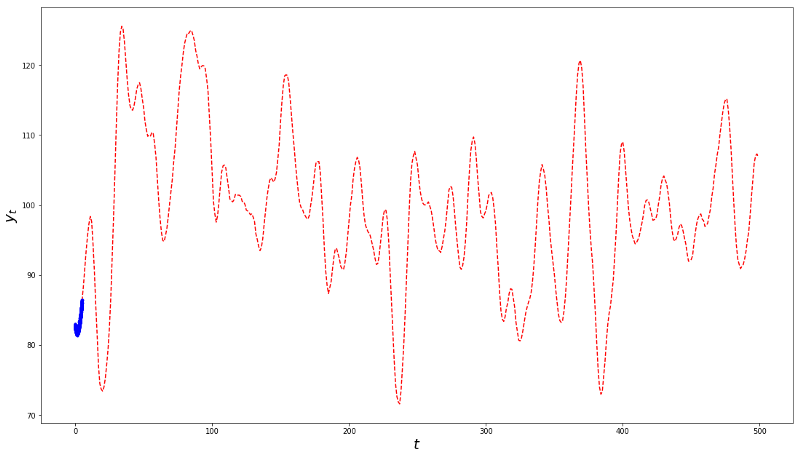
Exhibit 1 – Samples drawn from a Gaussian process with mean 100 and constant auto-covariance function
Why did the stationarity test “fail”? Because the blue sample is unrepresentative of the process. But the problem is not the test. The problem is the researcher, who has violated the representativeness assumption upon which the test is built. So to claim from this plot that “you shouldn’t trust any stationarity test” is a fallacious and unjustified conclusion.
The article argues that since one can never be sure that a nonstationary sample is representative of the process, one can never reject the hypothesis of stationarity, hence stationarity tests are useless. This argument is rather unconvincing. By the same token, since one can never be sure that a sample is representative of the process, one should never use statistics at all. How could one ever trust an average, if the sample may not be representative of the population? What’s more, if the article is correct, machine learning is also useless, and the organization publishing the article should cease to selling their services to their customers. How can one learn anything at all from samples that, alas, can never be complete? The answer, of course, is that researchers must make the assumption, not the statement, that data is representative. What is the basis for that assumption? The researcher’s specific knowledge of the observations. Field experts can make an informed assumption that a series is representative, based on their specialized knowledge of the observed sample.
As true followers of the “oracle paradigm” of ML, the organization publishing the article takes the position that expert-based assumptions of sample representativeness are unreliable. In their framework, scientific theories and expert knowledge should play no role in ML models. For them, data is all that matters. This argument is self-defeating because, if data is all that matters, then we cannot derive assumptions from theory, and without assumptions, quantitative tools cannot be used, hence data is useless.
After attacking stationarity tests, the organization set its crosshairs on differentiation. Differentiation is a standard procedure used by mathematicians to transform a nonstationary sample into a stationary one. However, mathematicians know that differentiation comes at a cost: A loss of past information that is relevant for future predictions, known as memory.
Think of memory in these terms: As a heavy weight stretches a spring, the spring “remembers” its equilibrium position, and pulls back the weight. That happens even if the spring is nonstationary, like the spring attached to a train. But in order to model the dynamics of the spring, we need to differentiate its observations, so that we work with a stationary series. However, that differentiation is not perfect, and it erases some information needed to determine how far the spring is from equilibrium. The solution to this “stationarity vs. memory dilemma” is to differentiate as little as needed to accomplish stationarity. One way statisticians resolve this dilemma is through fractional differentiation. But the organization that published the above article argues that since stationarity tests are useless anyway, the only thing differentiation accomplishes is a loss of memory. So again, they falsely conclude that differencing is useless, just like stationarity tests. Their advice is to work with nonstationary series, which is a recipe for overfitting: One cannot reliably train a ML algorithm on single-instance examples. The rest of their article and paper follow from these basic misunderstandings.
The implications of disregarding theory
What makes the above referenced article and paper so fascinating is that it offers a direct view into the mindset that often leads to backtest overfitting in finance (see also this Mathematical Investor blog on backtest overfitting in smart beta investments). Once a practitioner has no regard for economic theory, ML’s power to find any pattern (particularly spurious ones) goes unchecked. Combine that datamining power with the fact (again, predicted by theory) that arbitrage forces substantially reduce the signal-to-noise ratio, and false positives will readily be generated, whether or not the practitioner realizes it.
In the case of economics, finance and investments, theory is even more relevant than in natural sciences. The reason is that economic systems are human-made constructs. Economists have an unparalleled insight into the laws governing those phenomena. For example, microstructural theorists know how prices are formed: prices are the result of an auction mechanism that balances supply with demand. Economists do not need a statistical test to tell us that prices are nonstationary. Economists know that fact by construction, and the purpose of stationarity tests is to derive the amount of differentiation that achieves stationarity with minimum memory loss. Physicists do not have that advantage, because natural laws and systems are not human constructs — the laws of physics hold, at least in the measured reality sense, whether or not the universe contains even a single sentient individual capable of discovering those laws. That makes economic theories particularly powerful (and important) in setting realistic assumptions.
The key point that followers of the ML “oracle paradigm” miss is this: Financial series are much more easily overfit than physical series, because of the low signal-to-noise ratio that characterizes the former. Researchers’ best hope to avoid false positives is economic theory, particularly since economists enjoy the blessing of working on a field where systems are human-made, hence within our grasp.
In conclusion, ML and economic theory complement each other: Economic theory constrains ML’s propensity to overfit, and ML helps economists develop better theories, by uncovering complex interactions that exist among variables. Better theories lead to better forecasts. But theories should do the forecasting, not oracles. This is not different from the way scientists across all fields have been using ML for decades, to advance our understanding and improve upon previous knowledge. In stark contrast, the “oracle paradigm” disregards all economic theory for the false promise of better forecasts.
It is important for investors to understand why financial oracles are fundamentally flawed, and avoid falling victim of the unscientific promise of easy riches. In short: Beware of the hype. ML has an important role to play in finance, but it can never replace economic theory.